나비 효과

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 로렌츠 방정식과 로렌츠 어트랙터
3. 이론과 수학적 정의
4. 다양한 분야에서의 나비 효과
5. 대중 문화에서의 수용
참조

1. 개요

나비 효과는 역학계의 초기 조건에 아주 작은 변화가 발생해도 그 결과가 예측 불가능할 정도로 크게 달라지는 현상을 의미한다. 1898년 자크 아다마르가 궤도의 일반적인 차이를 지적한 것을 시작으로, 1960년대 에드워드 로렌츠의 기상 모의 실험을 통해 초기 조건의 미세한 차이가 결과에 엄청난 영향을 미칠 수 있다는 사실이 발견되었다. 로렌츠는 이 현상을 '나비 효과'라는 비유로 설명했는데, 브라질의 나비 날갯짓이 텍사스에 토네이도를 일으킬 수 있다는 비유가 널리 알려졌다. 이러한 나비 효과는 기상 예측, 양자역학, 사회 및 경제 현상 등 다양한 분야에서 나타나며, 대중 문화에서도 중요한 소재로 활용되고 있다.

더 읽어볼만한 페이지

안정성 이론 - 평형점
평형점은 미분 방정식 또는 차분 방정식에서 시간이 흘러도 변하지 않는 상태를 나타내는 점으로, 역학계의 안정성을 분석하는 데 중요한 역할을 하며, 쌍곡 평형점, 안정 평형점, 불안정 평형점, 안장점 등으로 분류된다.
안정성 이론 - 안장점
안장점은 다변수 실수 함수에서 어떤 방향으로는 극대, 다른 방향으로는 극소가 되는 점이며, 헤세 행렬을 통해 안장점 여부를 확인할 수 있고, 수학, 게임 이론, 최적화 문제 등 다양한 분야에서 활용된다.
혼돈 이론 - 창발
창발은 부분에는 없던 성질이 전체에서 나타나는 현상으로, 철학적으로는 요소의 속성으로 설명할 수 없는 체계의 특징을 의미하며, 복잡계 과학, 생명 현상 등 다양한 분야에서 중요한 개념으로 다뤄진다.
혼돈 이론 - 난류 (역학)
난류는 유체의 불규칙하고 무작위적인 운동 상태로, 일상생활과 공학 등 다양한 분야에서 관찰되며 여러 특징을 설명하기 위한 연구가 진행 중이다.

나비 효과
개요
브라질의 나비의 날갯짓이 텍사스에서 토네이도를 일으킬 수 있을까?

정의
설명	작은 원인이 결과에 큰 영향을 줄 수 있다는 개념
특징
관련 분야	기상학 카오스 이론
주요 내용	초기 조건의 미세한 차이가 예측 불가능한 결과를 초래할 수 있음
예시	날씨 예측의 불확실성 주식 시장의 변동성
역사
기원	에드워드 로렌츠의 카오스 이론 연구
어원	1963년 로렌츠의 논문 "결정론적 비주기적 흐름"에서 유래
대중화	로렌츠의 강연 "브라질에서 나비의 날갯짓이 텍사스에서 토네이도를 일으킬 수 있을까?"
과학적 의미
복잡계	초기 조건에 민감하게 반응하는 복잡계의 특성을 보여줌
예측 불가능성	완벽한 예측이 불가능함을 시사
대중 문화
영향	영화, 소설 등 다양한 분야에서 영감을 줌 "나비 효과"라는 용어가 널리 사용됨
주의 사항
오해	모든 작은 변화가 큰 결과를 초래하는 것은 아님
정확한 의미	특정 조건에서 초기 조건의 미세한 차이가 결과에 큰 영향을 줄 수 있다는 것
관련 개념
카오스 이론	카오스 이론
초기 조건 민감성	초기 조건에 따른 결과의 변화
추가 정보
로렌츠 어트랙터(나비효과)
로렌츠 어트랙터(나비효과)

2. 역사

카오스 이론의 핵심 개념 중 하나인 나비 효과는 초기 조건의 아주 작은 변화가 시간이 지남에 따라 예측할 수 없는 큰 차이를 만들어내는 현상을 가리킨다. 이 개념은 단순히 '작은 원인이 큰 결과를 낳는다'는 의미를 넘어, 결정론적 시스템이라 할지라도 초기 조건의 미세한 차이 때문에 장기적인 예측이 불가능함을 내포한다. 나비 효과라는 이름이 널리 알려지기까지 여러 과학자와 작가들의 기여가 있었다.

나비 효과에 대한 초기 아이디어는 19세기 말부터 논의되기 시작했다. 1890년 프랑스의 수학자 앙리 푸앵카레는 태양, 지구, 달의 궤도를 계산하는 삼체 문제를 연구하면서, 초기 조건의 미세한 변화가 결과적으로 궤도에 큰 차이를 유발할 수 있음을 발견했다. 그는 이러한 현상이 기상학처럼 복잡한 시스템에서도 나타날 수 있다고 제안했다.^[5]^[6] 이후 1898년 자크 아다마르는 특정 공간(음의 곡률 공간)에서 운동 궤적이 일반적으로 서로 멀어지는 경향(발산)을 보인다는 점을 지적했고, 1908년 피에르 뒤엠은 이러한 초기 조건 민감성이 과학 전반에 걸쳐 중요한 의미를 가질 수 있음을 논했다.^[5]

20세기 중반에도 유사한 아이디어가 등장했다. 1950년 영국의 수학자이자 컴퓨터 과학의 선구자인 앨런 튜링은 "단일 전자의 10억 분의 1cm 변위가 1년 후 눈사태로 인한 생사를 가를 수 있다"고 언급하며 극미한 변화의 증폭 가능성을 시사했다.^[7]

'나비 효과'라는 표현 자체는 1952년 미국의 작가 레이 브래드버리가 발표한 시간 여행 소재의 단편 소설 《천둥 소리(A Sound of Thunder)》에서 처음 사용된 것으로 알려져 있다.^[95]^[96] 소설 속에서 주인공은 과거로 시간 여행을 갔다가 실수로 나비 한 마리를 밟아 죽이는데, 현재로 돌아와 보니 역사가 완전히 뒤바뀌어 있었다는 내용을 담고 있다.^[8] 이는 작은 행위가 예상치 못한 거대한 결과를 초래할 수 있다는 나비 효과의 개념을 문학적으로 형상화한 초기 사례로 평가받는다.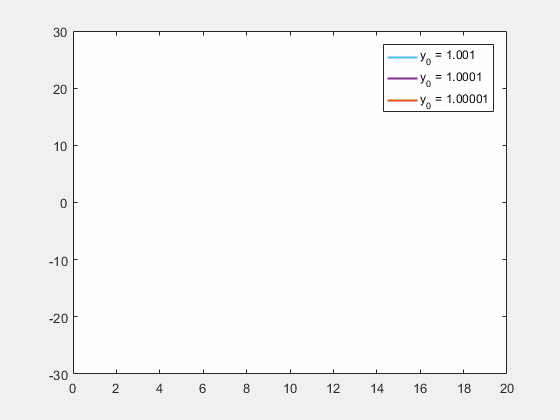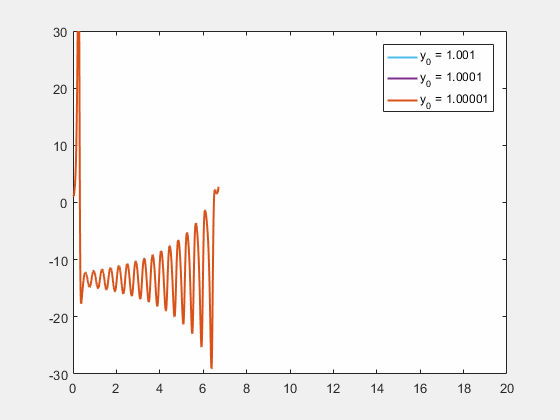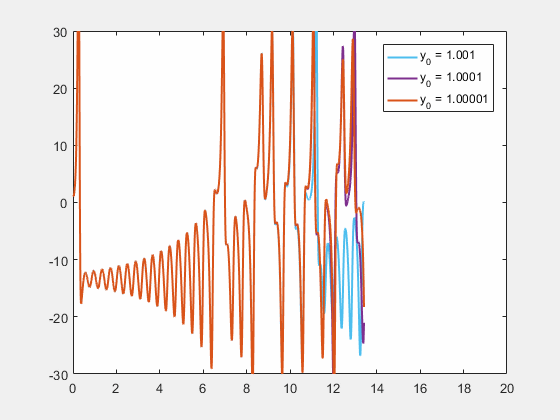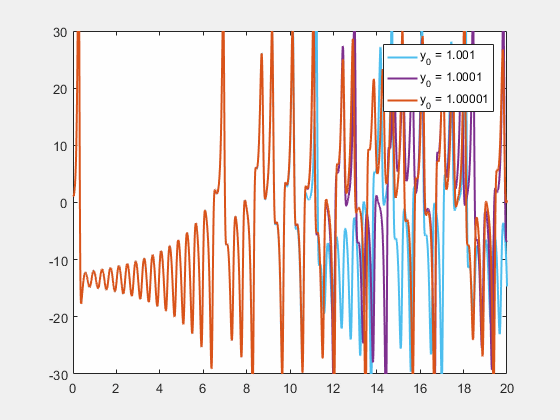

로렌츠 방정식에서의 초기값 민감성(나비 효과)의 예. 초기값이 아주 조금 다른 세 궤적(하늘색, 보라색, 주홍색)이 시간이 지남에 따라 완전히 다른 양상을 보이는 것을 보여준다.

과학계에서 나비 효과 개념이 본격적으로 주목받게 된 계기는 미국의 기상학자 에드워드 로렌츠의 연구였다. 1961년, 로렌츠는 컴퓨터를 이용해 날씨를 예측하는 수치 모델 실험 중, 초기 입력값의 미세한 차이(소수점 이하 몇 자리 생략)가 시간이 흐르면서 엄청나게 증폭되어 전혀 다른 날씨 패턴을 예측하는 결과를 우연히 발견했다.^[97]^[9] 이 발견은 결정론적 방정식으로 기술되는 시스템이라도 초기 조건에 극도로 민감하게 반응하여 장기 예측이 사실상 불가능할 수 있음을 시사했다.^[99]

로렌츠는 이 발견을 이론적으로 정리하여 1963년 미국 기상 학회 저널에 중요한 논문인 "결정론적 비주기적 흐름(Deterministic nonperiodic flow)"을 발표했다.^[3]^[11] 이 논문은 후일 카오스 이론 발전에 큰 영향을 주었다. 같은 해 발표한 다른 논문에서는 "만약 이론이 옳다면, 갈매기 한 마리의 날갯짓만으로도 날씨의 과정을 영원히 바꿀 수 있을 것"이라고 언급하며 초기 조건 민감성의 개념을 설명하기도 했다.^[13]^[67]

'나비 효과'라는 용어가 대중적으로 널리 퍼지게 된 것은 1972년 로렌츠가 미국 과학 진흥 협회(AAAS) 연례 회의에서 한 강연 덕분이었다. 당시 강연 제목을 정하지 못했던 로렌츠를 대신해 동료 기상학자 필립 메릴리스가 "예측가능성: 브라질에서의 한 나비의 날갯짓이 텍사스에 토네이도를 일으킬 수도 있는가?(Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas?)"라는 시적인 제목을 제안했다.^[1] 이 질문은 초기 조건의 작은 변화가 연쇄 반응을 통해 예상치 못한 큰 결과를 초래할 수 있다는 나비 효과의 개념을 상징적으로 잘 보여주었고, 이후 이 표현은 카오스 이론과 초기 조건 민감성을 설명하는 대표적인 용어로 자리 잡게 되었다.

나비 효과는 날씨 예측과 같이 초기 조건을 정확히 알기 어려운 복잡한 시스템의 예측 한계를 설명하는 데 중요한 개념으로 사용된다. 이러한 예측 불가능성 때문에 현대 기상 예보에서는 초기 조건을 약간씩 다르게 설정한 여러 시뮬레이션을 동시에 실행하여 확률적인 예측을 제공하는 앙상블 예측 기법이 개발되기도 했다.^[101]^[15]

2. 1. 로렌츠 방정식과 로렌츠 어트랙터

1961년 미국의 기상학자 에드워드 로렌츠는 컴퓨터로 기상 모의실험을 하던 중 초기 조건의 미세한 차이가 예상과 전혀 다른 결과를 낳는 현상을 발견했다. 처음 계산 시 입력값 "0.506127"을 사용했지만, 두 번째 계산에서는 컴퓨터 출력 과정에서 반올림된 값 "0.506"을 입력했다. 이 작은 차이가 시간이 지남에 따라 증폭되어 완전히 다른 기상 패턴을 예측하는 결과를 보였다.^[97] 로렌츠는 이를 통해 초기 조건에 극도로 민감하게 반응하는 시스템의 특성, 즉 초기 조건 민감성을 인지하게 되었다.^[99]

이러한 현상을 더 깊이 연구하기 위해 로렌츠는 기존의 복잡한 기상 모델 대신 더 단순화된 모델을 탐구했다. 동료 배리 잘츠먼의 연구에서 영감을 얻어, 그는 대기 순환을 설명하는 방정식을 단 3개의 변수로 줄인 모델을 개발했다. 이 연구 결과는 1963년 "결정론적 비주기적 흐름(Deterministic Nonperiodic Flow)"이라는 논문으로 발표되었으며, 여기에 제시된 3변수 연립 비선형 상미분 방정식이 바로 '''로렌츠 방정식'''이다.

:

\frac{dx}{dt} = -px+py

:

\frac{dy}{dt} = -xz+rx-y

:

\frac{dz}{dt} = xy-bz

위 식에서 ''x'', ''y'', ''z''는 시간에 따라 변하는 변수이며, ''p'', ''r'', ''b''는 시스템의 특성을 결정하는 매개변수(상수)이다. 로렌츠는 특정 매개변수 값(''p'' = 10, ''r'' = 28, ''b'' = 8/3)에서 이 방정식의 해가 매우 복잡하면서도 특정한 범위 내에서 움직이는 비주기적인 궤도를 그리는 것을 발견했다. 이 해의 궤도가 그리는 3차원 도형은 '''로렌츠 어트랙터'''(Lorenz attractor) 또는 '''로렌츠 끌개'''라고 불린다.^[65]

로렌츠 어트랙터는 카오스 이론에서 가장 유명한 예시 중 하나인 스트레인지 어트랙터이다. 이는 초기 조건이 아주 조금만 달라도 시간이 지남에 따라 궤적이 크게 달라지는 초기 조건 민감성을 명확하게 보여준다. 또한, 궤도는 특정 공간 내에 머무르지만 결코 스스로 교차하거나 동일한 패턴을 반복하지 않는 비주기적인 특징을 가진다.

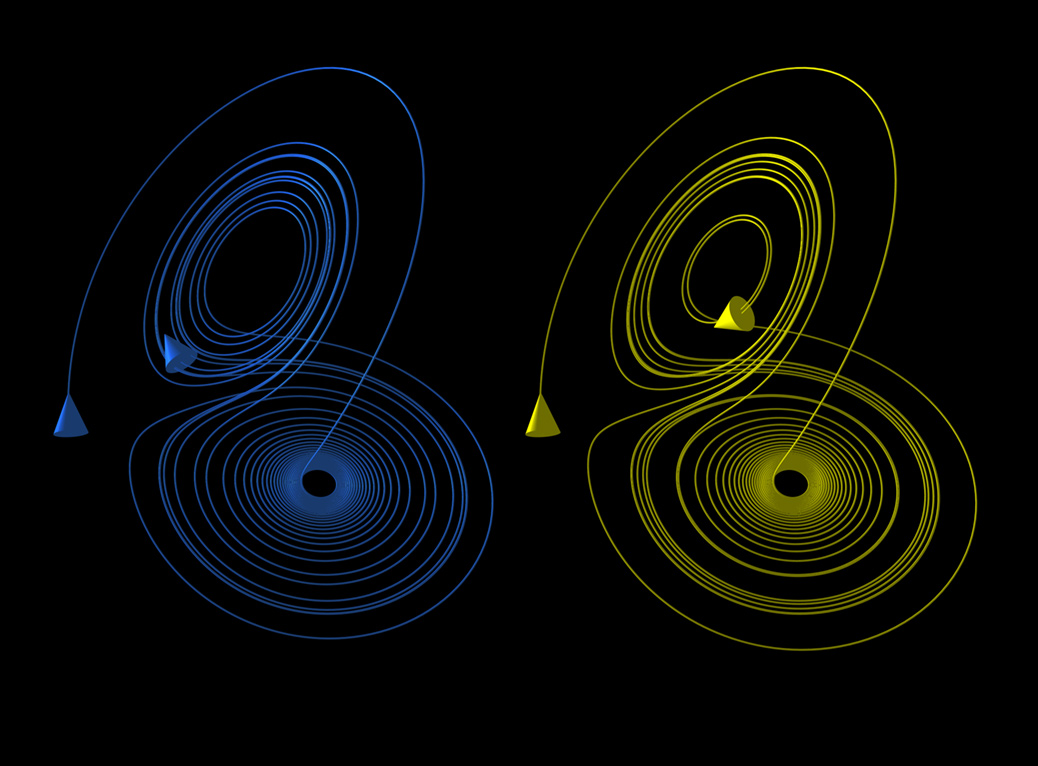
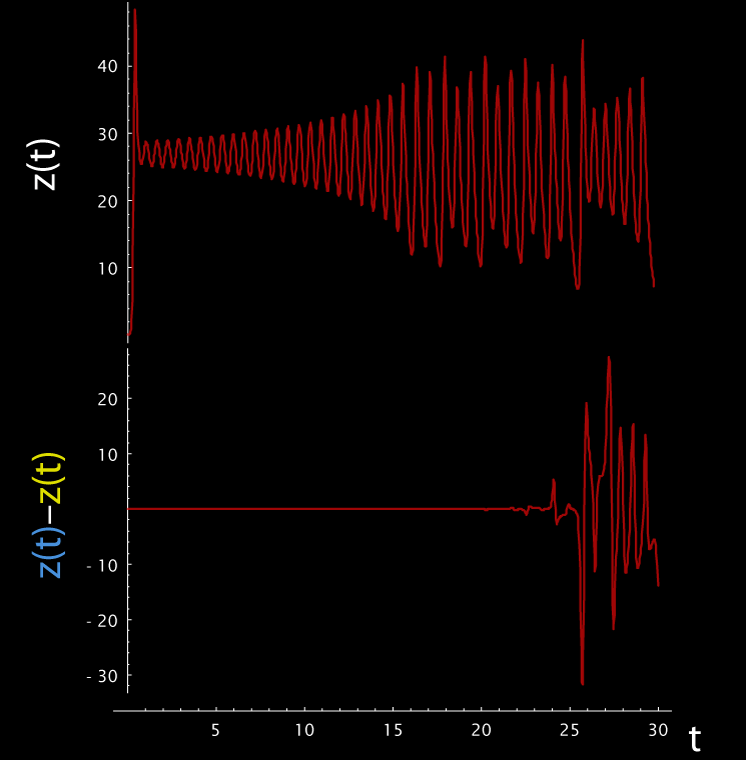
로렌츠 어트랙터에서 초기 조건이 10⁻⁵만큼 다른 두 궤적(파란색, 노란색)의 시간 변화 (0 ≤ ''t'' ≤ 30). 처음에는 거의 일치하지만 시간이 지나면서 크게 벌어진다.

위 두 궤적의 ''z'' 좌표 변화. 초기에는 차이가 미미하지만 ''t'' > 23 이후에는 차이가 매우 커짐을 보여준다.

흥미롭게도 로렌츠 어트랙터를 특정 각도에서 보면 마치 나비가 날개를 펼친 듯한 모양을 하고 있다. 이 때문에 '나비 효과'라는 이름이 로렌츠 어트랙터의 모양에서 유래했을 가능성도 제기된다. 로렌츠 자신도 이 가능성을 언급하며, 이 어트랙터가 '로렌츠 나비'라고도 불린다고 설명했다.

3. 이론과 수학적 정의

자연 현상은 시간의 경과에 따라 상태를 변화시킨다. 뉴턴 역학에서는 이러한 변화의 법칙, 즉 물체 운동의 법칙을 발견하고 미래 상태를 예측하는 방법을 확립했다. 어떤 상태의 다음 상태가 확정된 법칙에 따라 유일하게 결정된다는 이러한 생각은 결정론으로 알려져 있다. 양자역학의 등장으로 미시 세계에서는 상태 변화가 확률적으로 결정된다는 것이 밝혀졌지만, 일상적인 거시 세계의 많은 현상은 여전히 뉴턴 역학을 따른다. 이러한 결정론적 법칙에 기반하여 미래 상태를 예측하기 위해서는 계의 초기 상태(초기값) 정보가 필요하다. 라플라스의 악마는 완벽한 초기 상태 정보를 통해 과거와 미래의 모든 상태를 정확히 예측할 수 있다고 가정하지만, 현실에서는 초기 상태를 완전히 정확하게 아는 것이 불가능하다. 그럼에도 불구하고, 자연 과학 연구에서는 초기 상태의 오차가 미미하다면 최종 상태에서도 그 차이가 미미할 것이라고 가정하는 경우가 많았다. 그러나 카오스 현상의 발견으로, 결정론적 법칙을 따르는 시스템에서도 초기값의 아주 작은 차이가 예측할 수 없는 큰 차이를 만들어낼 수 있다는 사실이 밝혀졌다.^[62]

시간 경과에 따라 상태가 변하고, 그 변화 법칙이 결정론적으로 주어져 초기 상태가 정해지면 이후 상태가 유일하게 결정되는 시스템 또는 이를 다루는 수학 분야를 역학계라고 부른다. 역학계에서 초기 상태의 미세한 차이가 시간이 지남에 따라 지수 함수적으로 증가하여 무시할 수 없는 큰 차이를 만들 때, 그 계는 '''초기값 민감성'''을 갖는다고 한다. '''나비 효과'''는 이러한 초기값 민감성을 비유적으로 표현한 말이다. 초기값 민감성은 카오스 이론에서 말하는 '''카오스''' 현상의 주요 특징 중 하나이다. 다만, 초기값 민감성, 즉 지수 함수적으로 차이가 벌어지는 성질만으로는 카오스라고 불리지 않으며, 궤도가 유계 내에 갇혀 있는 것 등도 카오스의 요건이다. 대기 운동과 같은 현상은 비선형적인 역학계 방정식에 따르며 초기값 민감성을 갖는 것으로 여겨진다. 초기값 민감성 즉 나비 효과를 갖는지는, 랴푸노프 지수가 양의 값을 취하는지 등으로 정량 평가된다.

실제 자연 현상을 예측하기 위해 역학계 계산 모델을 사용할 때는 초기값이 필요하다. 하지만 관측을 통해 얻는 초기값에는 항상 오차가 포함될 수밖에 없다. 만약 예측 모델이 초기값 민감성을 가진다면, 아무리 작은 초기값 오차라도 시간이 지남에 따라 지수 함수적으로 커질 수 있다. 따라서 이러한 모델로는 단기간 내라면 어느 정도의 정밀도로 예측 가능해도 장기간 후의 상태 예측은 근사적으로도 불가능하다.^[62] 이러한 성질은 '''장기 예측 불능성'''^[62] 또는 '''예측 불가능성''' 등으로도 불린다. 이러한 초기값 민감성의 귀결인 장기 예측 불능성의 존재도, 나비 효과가 의미하는 것이다.

되돌이는 시스템이 초기 상태로 근사적으로 되돌아가는 현상이며, 초기 조건에 대한 민감한 의존성과 함께 카오스적 운동의 두 가지 주요 요소이다. 이는 복잡계가 일정 시간 범위(날씨의 경우 약 일주일) 이상 예측하기 어렵다는 실질적인 결과를 초래한다. 초기 대기 조건을 완전히 정확하게 측정하는 것이 불가능하기 때문이다.

역학계는 임의로 가까운 점들이 시간이 지남에 따라 지수적으로 분리될 경우 초기 조건에 민감한 의존성을 나타낸다. 이 정의는 위상적인 것이 아니라 본질적으로 계량적이다. 로렌츠^[25]는 민감한 의존성을 다음과 같이 정의했다.

''어떤 시점에서 그 점에 가까이 지나가는 대부분의 다른 궤도가 시간이 지남에 따라 그 점에 가까이 남아 있지 않으면 궤도(즉, 해)를 특징짓는 속성.''

만약 ''M''이 맵 $f^t$ 의 상태 공간이라면, $f^t$ 는 모든 x in ''M''과 모든 δ > 0에 대해 다음을 만족하는 거리 ''d''(. , .)를 갖는 ''M''의 y가 존재하면 초기 조건에 민감한 의존성을 나타낸다.

: $0 < d(x, y) < \delta$ 이고

다음이 성립한다.

: $d(f^\tau(x), f^\tau(y)) > \mathrm{e}^{a\tau} \, d(x,y)$

어떤 양의 매개변수 ''a''에 대해. 이 정의는 인접한 모든 점이 기준점 ''x''에서 분리될 것을 요구하지 않지만, 하나의 양의 랴푸노프 지수를 요구한다. 양의 랴푸노프 지수 외에도 유계성은 카오스적 시스템 내의 또 다른 주요 특징이다.^[26]

초기 조건에 민감한 의존성을 나타내는 가장 간단한 수학적 프레임워크는 로지스틱 맵의 특정 매개변수화에 의해 제공된다.

: $x_{n+1} = 4 x_n (1-x_n) , \quad 0\leq x_0\leq 1,$

이는 대부분의 카오스적 맵과 달리, 닫힌 형식 해를 갖는다.

: $x_{n}=\sin^{2}(2^{n} \theta \pi)$

여기서 초기 조건 매개변수 $\theta$ 는 $\theta = \tfrac{1}{\pi}\sin^{-1}(x_0^{1/2})$ 로 주어진다. 유리수 $\theta$ 의 경우, 유한한 횟수의 반복 후 $x_n$ 은 주기 수열으로 매핑된다. 그러나 거의 모든 $\theta$ 는 무리수이며, 무리수 $\theta$ 의 경우 $x_n$ 은 결코 반복되지 않으며 비주기적이다. 이 해 방정식은 카오스의 두 가지 주요 특징, 즉 스트레칭과 폴딩을 명확하게 보여준다. 2^''n''은 스트레칭의 지수적 성장을 나타내며, 이는 초기 조건에 대한 민감한 의존성(나비 효과)을 초래하는 반면, 제곱 사인 함수는 $x_n$ 을 범위 [0, 1] 내에서 접히도록 유지한다.

4. 다양한 분야에서의 나비 효과

(내용 없음 - 하위 섹션에서 상세 내용을 다루므로 중복을 피하기 위해 생략)

4. 1. 기상 예측

미국의 기상학자 에드워드 노턴 로렌즈는 1961년 컴퓨터로 기상 모의실험을 하던 중 초기 조건의 아주 작은 차이가 예측 결과에 엄청난 변화를 가져온다는 사실을 발견했다. 그는 소수점 아래 숫자를 일부 생략하고 입력했는데, 이 미세한 차이가 시간이 지남에 따라 증폭되어 전혀 다른 기상 예측 결과를 낳았다.^[97]^[9] 이 발견은 초기 조건에 대한 민감한 의존성, 즉 나비 효과의 핵심 개념으로 이어졌다.

나비 효과는 날씨와 같이 복잡하고 혼돈적인 시스템의 장기 예측이 근본적으로 어렵다는 것을 시사한다. 초기 대기 상태를 완벽하게 파악하는 것은 불가능하며, 아주 작은 관측 오차나 모델의 불완전성조차 시간이 흐르면서 예측의 정확도를 크게 떨어뜨리기 때문이다. 로렌츠는 이러한 현상을 설명하며 1972년 "브라질에서의 한 나비의 날갯짓이 텍사스에 돌풍을 일으킬 수도 있는가?"라는 제목의 강연을 통해 나비 효과를 대중에게 널리 알렸다. 이는 나비의 날갯짓이라는 작은 초기 변화가 연쇄적인 반응을 일으켜 토네이도와 같은 거대한 기상 현상의 발생 여부나 경로에 영향을 미칠 수 있다는 가능성을 시적으로 표현한 것이다.^[1]^[14] 물론 나비 자체가 토네이도를 만드는 것은 아니지만, 초기 조건의 미세한 변화가 결과적으로 큰 차이를 만들 수 있음을 의미한다.^[100]

이러한 예측의 불확실성 때문에 기상 예측 분야에서는 앙상블 예보 기법이 개발되었다. 앙상블 예보는 초기 조건에 의도적으로 약간의 변화를 준 여러 개의 예측 모델을 동시에 실행하고, 그 결과들을 종합하여 예측의 신뢰도를 높이는 방법이다.^[15]^[101] 초기값의 작은 차이가 시간이 지남에 따라 어떻게 예측 결과의 편차를 키우는지 보여줌으로써, 예측의 불확실성 범위를 파악하고 확률적인 정보를 제공할 수 있다.

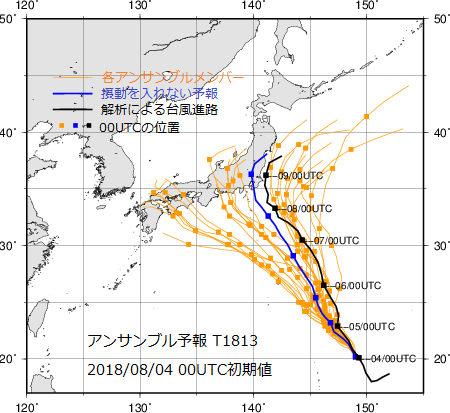
일본 기상청 등 여러 나라의 기상 기관에서는 태풍 진로 예측이나 중장기 날씨 예보에 앙상블 예보 기법을 적극적으로 활용하고 있다.^[75] 현재 상세한 일기 예보가 가능한 기간은 대략 2주 정도로 여겨지는데, 이는 나비 효과로 인한 예측 정확도 저하가 주요 원인 중 하나이다.^[70]^[73]

하지만 모든 과학자가 날씨 시스템이 로렌츠가 설명한 것만큼 초기 조건에 극도로 민감하다고 보지는 않는다. 일부 과학자들은 실제 날씨 예측 오류의 주된 원인이 초기 조건의 민감성보다는 기상 모델 자체의 불완전성이나 오류에 있다고 주장한다.^[16]^[17]^[18] 또한 로렌츠가 사용한 모델이 실제 대기 현상에 비해 매우 단순화되었다는 지적도 있다.^[19] 로렌츠 자신도 1972년 강연에서 나비 효과의 실제 영향력에 대한 명확한 답을 내리기보다는, 관측 시스템 개선과 연구 강화를 통해 예보 정확도를 높여야 할 필요성을 강조했다.^[63] 기상 예측의 오차는 초기값의 오차 증폭뿐만 아니라, 불완전한 관측, 관련 물리 법칙에 대한 이해 부족, 모델링 과정에서의 근사 등 복합적인 요인에 의해 발생한다.^[74]

결론적으로 나비 효과는 기상 예측의 한계를 설명하는 중요한 개념이지만, 실제 예측 정확도에 미치는 영향의 정도나 다른 요인과의 상대적 중요성에 대해서는 여전히 논의가 진행 중이다. 그럼에도 불구하고, 초기 조건의 민감성 문제는 앙상블 예보와 같은 새로운 예측 기법 개발을 촉진하는 등 현대 기상학 발전에 중요한 영향을 미쳤다.

4. 2. 양자역학

초기 조건에 대한 민감한 의존성, 즉 나비 효과가 양자역학과 반고전 물리학에서도 나타날 수 있는지에 대한 연구가 진행되었다. 예를 들어 강한 전자기장 속의 원자나 비등방성 케플러 문제 등이 연구 대상이었다.^[50]^[51]

일부 연구자들은 순수한 양자 시스템에서는 고전적인 카오스 이론에서 나타나는 극단적인(지수적인) 민감성이 나타나지 않을 것이라고 주장했다.^[52]^[53] 하지만 고전적 운동에서 나타나는 초기 조건 민감성은 마틴 구츠바일러^[54]나 존 B. 델로스^[55] 등이 개발한 반고전적 접근법을 통해 설명될 수 있다. 또한, 무작위 행렬 이론이나 양자 컴퓨터를 이용한 시뮬레이션 결과는 양자역학에서는 특정 형태의 나비 효과가 존재하지 않음을 시사하기도 했다.^[56]

반면, 나비 효과가 양자 시스템에서도 관찰될 수 있다고 주장하는 연구자들도 있다. 즈비그뉴 P. 카르쿠셰프스키(Zbigniew P. Karkuszewski) 연구팀은 서로 약간 다른 해밀토니안을 가진 양자 시스템의 시간 변화를 비교하며, 해밀토니안의 작은 변화가 시스템에 얼마나 큰 영향을 미치는지(민감도)를 조사했다.^[57] 데이비드 폴린(David Poulin) 연구팀은 '충실도 감소'를 측정하는 양자 알고리즘을 제시했는데, 이는 동일한 초기 상태가 약간 다른 동역학(해밀토니안) 하에서 얼마나 빠르게 달라지는지를 측정하는 방법이다. 연구팀은 이를 "고전적인 나비 효과에 가장 가까운 양자적 유사 현상"으로 보았다.^[58]

정리하자면, 고전적인 나비 효과는 주어진 해밀턴 시스템 내에서 물체의 초기 조건(위치, 속도 등)의 작은 변화가 이후 상태에 미치는 큰 영향을 다루는 반면, 양자 나비 효과는 동일한 초기 조건에서 시스템 자체(해밀토니안)의 작은 변화가 시간 경과에 따라 상태에 미치는 영향을 주로 다룬다.^[59]^[60] 이러한 양자 나비 효과는 실험을 통해서도 확인되었다.^[61] 초기 조건 민감성에 대한 양자역학적, 반고전적 연구 분야를 통틀어 양자 혼돈이라고 부른다.^[52]^[59]

4. 3. 사회, 경제 현상

나비 효과는 날씨와 같은 과학 현상뿐만 아니라 사회, 경제 분야에서도 그 영향을 관찰할 수 있다. 때로는 사소해 보이는 사건이 연쇄적인 파급 효과를 일으켜 예상치 못한 거대한 변화를 초래하기도 한다.

대표적인 예로 1930년대 세계 대공황은 미국 중서부 지역의 작은 은행 파산에서 시작되었으며, 2008년 세계 금융 위기 역시 캘리포니아의 작은 금융기관 파산이 발단이 된 것으로 알려져 있다.^[97] 이러한 사례들은 초기 작은 균열이 시스템 전체의 위기로 확산될 수 있음을 보여준다.

2011년 8월에는 국제 신용평가사인 스탠더드 앤드 푸어스가 미국의 재정 적자 문제를 이유로 국가 신용등급을 최고 등급인 AAA에서 AA+로 강등하는 사건이 발생했다.^[90] 미국의 신용등급 강등이라는 충격적인 소식은 즉각적으로 전 세계 금융시장에 영향을 미쳤다. 한국과 독일을 포함한 여러 나라의 주식 시장이 급락했고, 각국의 경제 성장률 전망치도 하향 조정되었다.^[90]

이 사건은 유럽 연합(EU) 국가들의 재정 건전성에 대한 불안감을 증폭시키는 계기가 되기도 했다. 특히 재정 위기를 겪고 있던 스페인 등 여러 국가의 신용등급이 연이어 하락했으며, 그리스는 결국 국가부도라는 심각한 상황을 맞았다.^[90] 이는 한 국가의 문제가 어떻게 국제적인 경제 위기로 번져나갈 수 있는지를 보여주는 나비 효과의 또 다른 사례라 할 수 있다.

5. 대중 문화에서의 수용

나비 효과는 카오스 이론과 초기 조건에 대한 민감한 의존성을 설명하는 개념으로, 수많은 문학 작품, 영화, 텔레비전, 비디오 게임 등 다양한 대중 매체에서 중요한 소재로 다루어져 왔다.^[5]^[6] 대중 문화에서 나비 효과는 종종 "역사와 운명을 결정하는 사소해 보이는 사건"이나 "인과 관계의 반복 끝에 인생의 행방이나 세계 경제에까지 영향을 미치는 첫 번째 계기"를 의미하는 은유로 사용되며^[64], 때로는 클리셰가 되기도 했다.^[64]

에드워드 로렌츠의 연구나 '나비 효과'라는 용어가 생기기 이전에도, 아주 작은 사건이 인과 관계를 통해 큰 결과로 이어질 수 있다는 아이디어는 여러 픽션 작품에서 나타났다. 예를 들어, 제임스 글릭은 그의 저서에서 동요 마더 구스의 '못이 없어서'를 이러한 오래된 예시로 들었다. 로렌츠 자신도 조지 R. 스튜어트의 1941년 소설 『폭풍』 등에서 유사한 개념을 찾아볼 수 있다고 언급했다.^[12]^[13]

그러나 저널리스트 피터 디자이크스(Peter Dizikes)는 대중 문화에서 나비 효과를 인용하는 방식이 이 개념의 한 측면만을 강조하는 경향이 있다고 지적했다.^[64]^[68] 즉, 나비의 날갯짓이 폭풍을 일으킬 수 있다는 단순한 인과 관계에만 초점을 맞추고, 로렌츠의 연구가 제시한 예측 불가능성이나 복잡한 시스템에서 원인을 특정하기 어렵다는 더 깊은 의미는 간과될 수 있다는 우려이다.^[64]

나비 효과를 중요한 줄거리나 설정으로 다루는 대표적인 작품들은 다음과 같다.

『천둥 소리』 (A Sound of Thunder): 1952년 레이 브래드버리가 발표한 SF 단편 소설.^[76] 시간 여행 중 실수로 나비 한 마리를 밟아 죽인 것이 역사를 크게 바꾸는 결과를 낳는다는 내용으로, 나비 효과의 개념을 상징적으로 보여주는 고전적인 예시로 자주 언급된다.^[77] 2005년에는 『사운드 오브 선더』라는 제목으로 영화화되었다.
『쥬라기 공원』 (Jurassic Park): 1990년 마이클 크라이튼의 SF 소설과 1993년 스티븐 스필버그 감독의 영화. 작중 이언 맬컴 박사가 카오스 이론과 나비 효과를 설명하며 공원의 위험성을 경고하고, 이는 이야기의 결말을 암시하는 역할을 한다.^[78]^[79] 이 작품은 당시 카오스 이론의 대중적 확산에 기여한 것으로 평가받는다.
『하바나』 (Havana): 1990년 영화. 로버트 레드포드가 연기한 주인공이 "한 마리의 나비가 중국에서 날갯짓하면 카리브에서 허리케인을 일으킨다"는 대사를 통해 나비 효과를 언급한다.^[64]
『나비 효과』 (The Butterfly Effect): 2004년 에릭 브레스와 J. 매키 그루버 감독의 SF 영화. 과거로 돌아가 자신의 행동을 바꿈으로써 현재와 미래를 바꾸려는 주인공의 이야기를 다루며, 영화 제목 자체가 나비 효과에서 유래했고 영화 전체의 핵심 모티브로 작용한다.^[80]^[81]^[82]
『미스터 노바디』 (Mr. Nobody): 2009년 자코 반 도르멜 감독의 SF 판타지 영화. 초끈 이론, 빅 크런치, 엔트로피 등 다양한 과학 이론과 함께 나비 효과를 영화의 중요한 구성 요소 및 스토리 전개의 기반으로 삼고 있다.^[83]^[84]^[85]
『그때 시작된 모든 것』: 2010년 나카무라 코우의 연애 소설.^[86] 이야기의 시작과 전개 방식이 나비 효과에 비유되며 평가받았다.^[87]^[88]
『라이프 이즈 스트레인지』 (Life Is Strange): 비디오 게임. 시간을 되돌리는 능력을 가진 주인공이 자신의 선택으로 인해 예상치 못한 결과를 마주하는 과정을 그리며 나비 효과를 핵심 메커니즘으로 사용한다.
『ZERO ESCAPE 딜레마의 시간』: 2016년 스파이크 춘소프트의 게임. "운명이란 잔혹한 것이다. 단 한 마리의 달팽이가 세계를 멸망시킬 수도 있다"는 대사를 통해 나비 효과를 암시한다.^[89]
기타: TV 시리즈 『심슨 가족』, 웹코믹 『홈스턱』 등에서도 나비 효과를 소재로 한 에피소드나 설정이 등장한다.

참조

_[1] 웹사이트 Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas? https://mathscienceh[...] 2021-12-23
_[2] 웹사이트 When Lorenz Discovered the Butterfly Effect https://www.bbvaopen[...] 2021-12-23
_[3] 논문 Deterministic Nonperiodic Flow 1963-03
_[4] 간행물 Butterfly effect http://www.scholarpe[...] 2009-05-04
_[5] 웹사이트 Some Historical Notes: History of Chaos Theory https://www.wolframs[...]
_[6] 서적 The Restless Universe Applications of Gravitational N-Body Dynamics to Planetary Stellar and Galactic Systems https://books.google[...] CRC Press 2001-09
_[7] 웹사이트 Computing Machinery and Intelligence https://academic.oup[...]
_[8] 웹사이트 The Physics of Ray Bradbury's "A Sound of Thunder" https://www.inquirer[...] 2015-09-02
_[9] 서적 Chaos: Making a New Science Viking 1987
_[10] 논문 Chaos at fifty 2013
_[11] 웹사이트 Google Scholar citation record https://scholar.goog[...]
_[12] 웹사이트 Part19 http://www.cs.ualber[...] Cs.ualberta.ca 1960-11-22
_[13] 논문 The Predictability of Hydrodynamic Flow https://eapsweb.mit.[...] 1963
_[14] 웹사이트 The Butterfly Effects – What Does It Really Signify? http://blog.ap42.com[...]
_[15] 서적 Medium-range weather prediction: The European approach; The story of the European Centre for Medium-Range Weather Forecasts https://archive.org/[...] Springer 2005
_[16] 논문 Model error in weather forecasting 2001
_[17] 논문 Role of the metric in forecast error growth: How chaotic is the weather? 2002
_[18] 서적 Truth or Beauty: Science and the Quest for Order Yale University Press 2012
_[19] 서적 A New Kind of Science https://archive.org/[...] Wolfram Media 2002
_[20] 논문 Aggregated Negative Feedback in a Generalized Lorenz Model 2019
_[21] 논문 The predictability of a flow which possesses many scales of motion 1969-06
_[22] Youtube The Butterfly Effect – What Does It Really Signify? https://www.youtube.[...] 2017-05-19
_[23] Youtube Edward N. Lorenz and the End of the Cartesian Universe https://www.youtube.[...] 2018-03-26
_[24] 논문 One Saddle Point and Two Types of Sensitivities within the Lorenz 1963 and 1969 Models 2022-05-07
_[25] 서적 The essence of chaos https://www.worldcat[...] UCL Press 1993
_[26] 서적 Nonlinear ordinary differential equations: an introduction for scientists and engineers https://www.worldcat[...] Oxford Univ. Press 2011
_[27] 웹사이트 Chaos and Climate https://www.realclim[...] RealClimate 2005-11-04
_[28] 논문 Nonlinear Feedback in a Five-Dimensional Lorenz Model https://journals.ame[...] 2014-05-01
_[29] 논문 Revisiting Lorenz's and Lilly's Empirical Formulas for Predictability Estimates https://egusphere.co[...] 2024-07-24
_[30] 논문 Three Kinds of Butterfly Effects within Lorenz Models 2022-07-04
_[31] 논문 Can the Flap of a Butterfly's Wings Shift a Tornado into Texas—Without Chaos? 2023-05-02
_[32] 논문 The Butterfly Effect: Can a butterfly in Brazil cause a tornado in Texas? https://doi.org/10.1[...] 2024-05-01
_[33] 논문 The real butterfly effect and maggoty apples 2024-05-01
_[34] 논문 Butterfly effects https://pubs.aip.org[...] 2024-09-01
_[35] 논문 Butterfly effects https://pubs.aip.org[...] 2024-09-01
_[36] 논문 Summary of Two Kinds of Butterfly Effects https://rgdoi.net/10[...] 2024-09-02
_[37] 논문 The recently recognized failure of predictability in Newtonian dynamics http://dx.doi.org/10[...] 1986-09-08
_[38] 논문 Lorenz's View on the Predictability Limit of the Atmosphere 2023-07-22
_[39] 서적 The Feasibility of a Global Observation and Analysis Experiment http://dx.doi.org/10[...] 1966-01-01
_[40] 논문 A Guide to GARP 1969-03-01
_[41] 웹사이트 Lorenz's View on the Predictability Limit. https://encyclopedia[...] 2023-09-13
_[42] 논문 Exploring the Origin of the Two-Week Predictability Limit: A Revisit of Lorenz's Predictability Studies in the 1960s 2024-07-16
_[43] 논문 Is Weather Chaotic?: Coexistence of Chaos and Order within a Generalized Lorenz Model 2021-01-01
_[44] 서적 13th Chaotic Modeling and Simulation International Conference Springer International Publishing 2021
_[45] 논문 Predictability and Predictions 2022-08-14
_[46] 간행물 Chaos in Classical Mechanics: The Double Pendulum https://link.springe[...] Springer Berlin Heidelberg 2022-07-11
_[47] 논문 Chaos in a double pendulum https://doi.org/10.1[...] 1992
_[48] 논문 The Dual Nature of Chaos and Order in the Atmosphere 2022-11-12
_[49] Youtube Exploring Chaos Theory for Monstability and Multistability https://www.youtube.[...] 2023-02-21
_[50] 논문 Postmodern Quantum Mechanics 1993-07
_[51] 서적 Chaos in Classical and Quantum Mechanics Springer-Verlag
_[52] 웹사이트 What is... Quantum Chaos? https://www.ams.org/[...] 2008-01
_[53] 논문 Quantum chaology, not quantum chaos
_[54] 논문 Periodic Orbits and Classical Quantization Conditions
_[55] 논문 Closed-orbit theory of oscillations in atomic photoabsorption cross sections in a strong electric field. II. Derivation of formulas https://scholarworks[...]
_[56] 논문 Recovery of Damaged Information and the Out-of-Time-Ordered Correlators
_[57] 논문 Quantum Chaotic Environments, the Butterfly Effect, and Decoherence
_[58] 논문 Exponential Speedup with a Single Bit of Quantum Information: Measuring the Average Fidelity Decay
_[59] 웹사이트 A Rough Guide to Quantum Chaos http://www.iqc.ca/pu[...]
_[60] 서적 Quantum Theory: Concepts and Methods Kluwer Academic
_[61] 논문 Quantum amplifier: Measurement with entangled spins
_[62] 서적 カオス時系列解析の基礎と応用産業図書
_[63] 웹사이트 Predictability: Does the Flap of a Butterfly's Wings in Brazil Set Off a Tornado in Texas? http://eaps4.mit.edu[...] 2014-12-28
_[64] 뉴스 The meaning of the butterfly: Why pop culture loves the 'butterfly effect,' and gets it totally wrong http://www.boston.co[...] Globe Newspaper Company 2008-06-08
_[65] 서적 カオス力学の基礎 https://www.gensu.jp[...] 現代数学社
_[66] 서적 Chaos, Complexity and Leadership 2013 https://books.google[...] Springer International Publishing
_[67] 논문 The predictability of hydrodynamic flow. http://eaps4.mit.edu[...]
_[68] 뉴스 When the Butterfly Effect Took Flight http://www.technolog[...] MIT Technology Review 2011-02-22
_[69] 서적 世界はデタラメ ―ランダム宇宙の科学と生活 https://www.nttpub.c[...] NTT出版
_[70] 웹사이트 長期予報はなぜ当たらないか http://wwwoa.ees.hok[...] 2015-01-11
_[71] 웹사이트 コンピューターによる天気の長期予報 https://web.archive.[...] NHK 2015-01-11
_[72] 서적 応用カオス ―カオスそして複雑系へ挑む https://www.saiensu.[...] サイエンス社
_[73] 서적 嵐の正体にせまった科学者たち―気象予報が現代のかたちになるまで https://www.maruzen-[...] 丸善出版
_[74] 웹사이트 アンサンブル予報 https://www.jma.go.j[...] 2021-08-11
_[75] 웹사이트 知識・解説アンサンブル予報 https://www.jma.go.j[...] 気象庁 2021-08-11
_[76] 웹사이트 雷のような音とは - デジタル大辞泉プラスの解説 https://kotobank.jp/[...] 朝日新聞 / VOYAGE GROUP 2015-09-19
_[77] 웹사이트 The Physics of Ray Bradbury's "A Sound of Thunder" http://www.philly.co[...] Philadelphia Media Network 2015-09-19
_[78] 서적 ジュラシック・パーク〈上〉早川書房 1993-03-31
_[79] Youtube Jurassic Park (2/10) Movie CLIP - Chaos Theory (1993) HD https://www.youtube.[...] Universal 2015-05-17
_[80] 웹사이트 『バタフライ・エフェクト』- 作品情報 - 映画シネマトゥデイ https://www.cinemato[...] シネマトゥデイ 2015-05-05
_[81] 웹사이트 映画バタフライ・エフェクト - 作品情報 - allcinema https://www.allcinem[...] スティングレイ 2015-05-05
_[82] 웹사이트 バタフライ・エフェクト－映画作品紹介－ CINEMA TOPICS ONLINE http://www.cinematop[...] CINEMA TOPICS ONLINE 2015-05-05
_[83] 웹사이트 ジャコ・ヴァン・ドルマル『ミスター・ノーバディ』レビュー http://www.outsidein[...] OUTSIDE IN TOKYO 2015-08-10
_[84] 웹사이트 Jaco van Dormael - The return of a hero http://www.independe[...] The Independent 2015-08-10
_[85] 웹사이트 TIFF 09 Review: Mr Nobody http://www.rowthree.[...] Row Three 2015-08-10
_[86] 웹사이트 あのとき始まったことのすべて http://www.kadokawa.[...] KADOKAWA 2015-09-19
_[87] 웹사이트 【書評】『あのとき始まったことのすべて』中村航 - 横丁カフェ - WEB本の雑誌 http://www.webdoku.j[...] 本の雑誌社/博報堂 2015-05-05
_[88] 웹사이트 読書のいずみ - 読書マラソン２０選 - ナイスランナー賞 http://www.univcoop.[...] 全国大学生活協同組合連合会 2015-05-05
_[89] 웹사이트 ZERO CHARACTER https://www.spike-ch[...] スパイク・チュンソフト 2020-01-08
_[90] 네이버지식백과 "[네이버 지식백과] 나비효과 [Butterfly effect] (상식으로 보는 세상의 법칙" https://terms.naver.[...]
_[91] 다음백과 "[ 다음백과 ] 나비 효과 (Butterfly Effect)" https://100.daum.net[...]
_[92] 다음백과 "[ 다음백과 TTA정보통신용어사전 '' 나비 효과 (Butterfly Effect)]" https://100.daum.net[...]
_[93] 네이버지식백과 "[네이버 지식백과] 나비효과 (박경미의 수학콘서트 플러스, 2013. 12. 12., 박경미)" https://terms.naver.[...]
_[94] 네이버지식백과 "[네이버 지식백과] 나비효과 (매일경제, 매경닷컴)" https://terms.naver.[...]
_[95] 웹사이트 Some Historical Notes: History of Chaos Theory http://www.wolframsc[...]
_[96] 서적 The Restless Universe Applications of Gravitational N-Body Dynamics to Planetary Stellar and Galactic Systems http://books.google.[...] CRC Press 2014-01-06
_[97] 네이버지식백과 "[네이버 지식백과] 작은 변화가 후폭풍을 부른다 - 나비 효과 (시장의 흐름이 보이는 경제 법칙 101, 2011. 2. 28., 김민주)" https://terms.naver.[...]
_[98] 네이버지식백과 나비효과 (매일경제, 매경닷컴)
_[99] 서적 이즘과 올로지 랜덤하우스코리아 2009-12-04
_[100] 웹인용 The Butterfly Effects: Variations on a Meme https://web.archive.[...] 2011-08-03
_[101] 서적 Medium-range weather prediction: The European approach; The story of the European Centre for Medium-Range Weather Forecasts Springer
_[102] 웹인용 A Rough Guide to Quantum Chaos https://web.archive.[...] 2009-08-12